Fourier series expansion of a quadratic function. Fourier series expansion of even and odd functions Bessel’s inequality Parseval’s equality

The Fourier series of an even periodic function f(x) with period 2p contains only terms with cosines (i.e., does not contain terms with sines) and may include a constant term. Hence,

where are the coefficients of the Fourier series,

The Fourier series of an odd periodic function f (x) with period 2p contains only terms with sines (that is, it does not contain terms with cosines).

Hence,

where are the coefficients of the Fourier series,

If a function is defined for a range, say from 0 to p, and not just from 0 to 2p, it can be expanded into a series only in sines or only in cosines. The resulting Fourier series is called the half-cycle Fourier series.

If you want to obtain a half-cycle Fourier expansion of the cosines of the function f (x) in the range from 0 to p, then you need to construct an even periodic function. In Fig. Below is the function f (x) = x, built on the interval from x = 0 to x = p. Since the even function is symmetrical about the f (x) axis, we draw line AB, as shown in Fig. below. If we assume that outside the considered interval the resulting triangular shape is periodic with a period of 2p, then the final graph looks like this: in Fig. below. Since we need to obtain the Fourier expansion in cosines, as before, we calculate the Fourier coefficients a o and a n

If you want to obtain the Fourier expansion on a half-cycle in terms of the sines of the function f (x) in the range from 0 to p, then you need to construct an odd periodic function. In Fig. Below is the function f (x) =x, built on the interval from x=0 to x=p. Since odd function symmetrical about the origin of coordinates, we construct the line CD, as shown in Fig.

If we assume that outside the considered interval the resulting sawtooth signal is periodic with a period of 2p, then the final graph has the form shown in Fig. Since we need to obtain the Fourier expansion of the half-cycle in terms of sines, as before, we calculate the Fourier coefficient. b

Fourier series expansion of even and odd functions expansion of a function given on an interval into a series in sines or cosines Fourier series for a function with an arbitrary period Complex representation of the Fourier series Fourier series in general orthogonal systems of functions Fourier series in an orthogonal system Minimal property of Fourier coefficients Bessel’s inequality Equality Parseval Closed systems Completeness and closedness of systems

Fourier series expansion of even and odd functions A function f(x), defined on the interval \-1, where I > 0, is called even if the graph of the even function is symmetrical about the ordinate axis. A function f(x), defined on the segment J), where I > 0, is called odd if the graph of the odd function is symmetrical with respect to the origin. Example. a) The function is even on the interval |-jt, jt), since for all x e b) The function is odd, since Fourier series expansion of even and odd functions is expansion of a function given on an interval into a series in sines or cosines. Fourier series for a function with an arbitrary period Complex representation of the Fourier series Fourier series for general orthogonal systems of functions Fourier series for an orthogonal system Minimal property of Fourier coefficients Bessel’s inequality Parseval’s equality Closed systems Completeness and closedness of systems c) Function f(x)=x2-x, where does not belong neither to even nor to odd functions, since Let the function f(x), satisfying the conditions of Theorem 1, be even on the interval x|. Then for everyone i.e. /(x) cos nx is an even function, and f(x) sinnx is an odd one. Therefore, the Fourier coefficients of an even function f(x) will be equal. Therefore, the Fourier series of an even function has the form f(x) sin х - an even function. Therefore, we will have Thus, the Fourier series of an odd function has the form Example 1. Expand the function 4 into a Fourier series on the interval -x ^ x ^ n Since this function is even and satisfies the conditions of Theorem 1, then its Fourier series has the form Find the Fourier coefficients. We have Applying integration by parts twice, we obtain that So, the Fourier series of this function looks like this: or, in expanded form, This equality is valid for any x €, since at the points x = ±ir the sum of the series coincides with the values ​​of the function f(x ) = x2, since the graphs of the function f(x) = x and the sum of the resulting series are given in Fig. Comment. This Fourier series allows us to find the sum of one of the convergent numerical series, namely, for x = 0 we obtain that Example 2. Expand the function /(x) = x into a Fourier series on the interval. The function /(x) satisfies the conditions of Theorem 1, therefore it can be expanded into a Fourier series, which, due to the oddness of this function, will have the form Integrating by parts, we find the Fourier coefficients Therefore, the Fourier series of this function has the form This equality holds for all x B at points x - ±t the sum of the Fourier series does not coincide with the values ​​of the function /(x) = x, since it is equal to. Outside the interval [-*, i-] the sum of the series is a periodic continuation of the function /(x) = x; its graph is shown in Fig. 6. § 6. Expansion of a function given on an interval into a series in sines or cosines Let a bounded piecewise monotonic function / be given on the interval. The values ​​of this function on the interval 0| can be further defined in various ways. For example, you can define a function / on the segment tc] so that /. In this case they say that) “is extended to the segment 0] in an even manner”; its Fourier series will contain only cosines. If the function /(x) is defined on the interval [-l-, mc] so that /(, then the result is an odd function, and then they say that / is “extended to the interval [-*, 0] in an odd way”; in this In this case, the Fourier series will contain only sines. Thus, each bounded piecewise monotonic function /(x) defined on the interval can be expanded into a Fourier series in both sines and cosines. Example 1. The function can be expanded into a Fourier series: a) by cosines; b) by sines. M This function, with its even and odd continuations into the segment |-x,0) will be bounded and piecewise monotonic. a) Let's extend /(z) into the segment 0) a) Extend j\x) into the segment (-тр,0| in an even manner (Fig. 7), then its Fourier series i will have the form П=1 where the Fourier coefficients are equal, respectively for Therefore, b) Let us extend /(z) into the segment [-x,0] in an odd way (Fig. 8). Then its Fourier series §7. Fourier series for a function with an arbitrary period Let the function fix) be periodic with a period of 21.1 ^ 0. To expand it into a Fourier series on the interval where I > 0, we make a change of variable by setting x = jt. Then the function F(t) = / ^tj will be a periodic function of the argument t with period and it can be expanded on the segment into a Fourier series. Returning to the variable x, i.e., setting, we obtain All theorems valid for Fourier series of periodic functions with period 2π , remain valid for periodic functions with an arbitrary period 21. In particular, a sufficient criterion for the decomposability of a function in a Fourier series also remains valid. Example 1. Expand into a Fourier series a periodic function with a period of 21, given on the interval [-/,/] by the formula (Fig. 9). Since this function is even, its Fourier series has the form Substituting the found values ​​of the Fourier coefficients into the Fourier series, we obtain We note one thing important property periodic functions. Theorem 5. If a function has period T and is integrable, then for any number a the equality m holds. that is, the integral of a segment whose length is equal to the period T has the same value regardless of the position of this segment on the number axis. In fact, We make a change of variable in the second integral, assuming. This gives and therefore, Geometrically, this property means that in the case of the area shaded in Fig. 10 areas are equal to each other. In particular, for a function f(x) with a period we obtain at Expansion into a Fourier series of even and odd functions, expansion of a function given on an interval into a series in sines or cosines Fourier series for a function with an arbitrary period Complex notation of the Fourier series Fourier series in general orthogonal systems functions Fourier series in an orthogonal system Minimal property of Fourier coefficients Bessel’s inequality Parseval’s equality Closed systems Completeness and closedness of systems Example 2. The function x is periodic with a period Due to the oddness of this function, without calculating integrals, we can state that for any The proven property, in particular, shows that the Fourier coefficients of a periodic function f(x) with a period of 21 can be calculated using the formulas where a is an arbitrary real number (note that the functions cos - and sin have a period of 2/). Example 3. Expand into a Fourier series a function given on an interval with a period of 2x (Fig. 11). 4 Let's find the Fourier coefficients of this function. Putting in the formulas we find that for Therefore, the Fourier series will look like this: At the point x = jt (discontinuity point of the first kind) we have §8. Complex recording of the Fourier series This section uses some elements of complex analysis (see Chapter XXX, where all actions performed here with complex expressions are strictly justified). Let the function f(x) satisfy sufficient conditions for expansion into a Fourier series. Then on the segment x] it can be represented by a series of the form Using Euler’s formulas Substituting these expressions in series (1) instead of cos πx and sin φx we will have Let us introduce the following notation Then series (2) will take the form Thus, the Fourier series (1) is represented in complex form (3). Let's find expressions for the coefficients through integrals. We have Similarly, we find The final formulas for с„, с_п and с can be written as follows: . . The coefficients с„ are called the complex Fourier coefficients of the function. For a periodic function with a period), the complex form of the Fourier series will take the form where the coefficients Cn are calculated using the formulas. The convergence of series (3) and (4) is understood as follows: series (3) and (4) are called convergent for given value g, if there are limits Example. Expand the period function into a complex Fourier series. This function satisfies sufficient conditions for expansion into a Fourier series. Let us find the complex Fourier coefficients of this function. We have for odd for even n, or, in short. Substituting the values), we finally obtain Note that this series can also be written as follows: Fourier series for general orthogonal systems of functions 9.1. Orthogonal systems of functions Let us denote by the set of all (real) functions defined and integrable on the interval [a, 6] with a square, i.e., those for which an integral exists. In particular, all functions f(x) continuous on the interval [a , 6], belong to 6], and the values ​​of their Lebesgue integrals coincide with the values ​​of the Riemann integrals. Definition. A system of functions, where, is called orthogonal on the interval [a, b\, if Condition (1) assumes, in particular, that none of the functions is identically zero. The integral is understood in the Lebesgue sense. and we call the quantity the norm of the function. If in an orthogonal system for any n we have, then the system of functions is called orthonormal. If the system (y>„(x)) is orthogonal, then the system Example 1. The trigonometric system is orthogonal on a segment. The system of functions is an orthonormal system of functions on, Example 2. The cosine system and the sine system are orthonormal. Let us introduce the notation that they are orthogonal on the interval (0, f|, but not orthonormal (for I Ф- 2). Since their norms are COS Example 3. Polynomials defined by equality are called Legendre polynomials (polynomials). For n = 0 we have It can be proven that the functions form an orthonormal system of functions on the interval. Let us show, for example, the orthogonality of the Legendre polynomials. Let m > n. In this case, integrating n times by parts, we find since for the function t/m = (z2 - I)m all derivatives up to of order m - I inclusive vanish at the ends of the segment [-1,1). Definition. A system of functions (pn(x)) is called orthogonal on the interval (a, b) by an overhang p(x) if: 1) for all n = 1,2,... there are integrals. Here it is assumed that the weight function p(x) is defined and positive everywhere on the interval (a, b) with the possible exception of a finite number of points where p(x) can vanish. Having performed differentiation in formula (3), we find. It can be shown that the Chebyshev-Hermite polynomials are orthogonal on the interval Example 4. The system of Bessel functions (jL(pix)^ is orthogonal on the interval zeros of the Bessel function Example 5. Let us consider the Chebyshev-Hermite polynomials, which can be defined using equality. Fourier series in an orthogonal system Let there be an orthogonal system of functions in the interval (a, 6) and let the series (cj = const) converge on this interval to the function f(x): Multiplying both sides of the last equality by - fixed) and integrating over x from a to 6, due to the orthogonality of the system, we obtain that this operation has, generally speaking, a purely formal character. However, in some cases, for example, when the series (4) converges uniformly, all functions are continuous and the interval (a, 6) is finite, this operation is legal. But for us now it is the formal interpretation that is important. So, let a function be given. Let's form numbers c* using formula (5) and write. The series on the right side is called near Fourier functions f(x) with respect to the system (^n(i)) - The numbers Cn are called the Fourier coefficients of the function f(x) with respect to this system. The sign ~ in formula (6) only means that the numbers Cn are related to the function f(x) by formula (5) (it is not assumed that the series on the right converges at all, much less converges to the function f(x)). Therefore, the question naturally arises: what are the properties of this series? In what sense does it “represent” the function f(x)? 9.3. Convergence on average Definition. A sequence converges to the element ] on average if the norm is in the space Theorem 6. If a sequence ) converges uniformly, then it converges on average. M Let the sequence ()) converge uniformly on the interval [a, b] to the function /(x). This means that for everyone, for all sufficiently large n, we have Therefore, from which our statement follows. The converse is not true: the sequence () may converge on average to /(x), but not be uniformly convergent. Example. Consider the sequence nx. It is easy to see that But this convergence is not uniform: there exists e, for example, such that, no matter how large n is, on the interval cosines Fourier series for a function with an arbitrary period Complex representation of the Fourier series Fourier series for general orthogonal systems of functions Fourier series for an orthogonal system Minimal property of Fourier coefficients Bessel’s inequality Parseval’s equality Closed systems Completeness and closedness of systems and let We denote by c* the Fourier coefficients of the function /(x ) by an orthonormal system b Consider a linear combination where n ^ 1 is a fixed integer, and find the values ​​of the constants at which the integral takes a minimum value. Let us write it in more detail. Integrating term by term, due to the orthonormality of the system, we obtain. The first two terms on the right side of equality (7) are independent, and the third term is non-negative. Therefore, the integral (*) takes a minimum value at ak = sk. The integral is called the mean square approximation of the function /(x) by a linear combination of Tn(x). Thus, the root mean square approximation of the function /\ takes on a minimum value when. when Tn(x) is the 71st partial sum of the Fourier series of the function /(x) over the system (. Setting ak = sk, from (7) we obtain Equality (9) is called the Bessel identity. Since its left side is non-negative, then from it Bessel’s inequality follows. Since I am here arbitrarily, Bessel’s inequality can be represented in a strengthened form, i.e. that is, for any function / the series of squared Fourier coefficients of this function in an orthonormal system ) converges. Since the system is orthonormal on the interval [-x, m], then inequality (10) translated into the usual notation of the trigonometric Fourier series gives the relation do that is valid for any function /(x) with an integrable square. If f2(x) is integrable, then due to necessary condition convergence of the series on the left side of inequality (11), we obtain that. Parseval's equality For some systems (^„(x)), the inequality sign in formula (10) can be replaced (for all functions f(x) 6 ×) by an equal sign. The resulting equality is called the Parseval-Steklov equality (completeness condition). Bessel's identity (9) allows us to write condition (12) in an equivalent form. Thus, the fulfillment of the completeness condition means that the partial sums Sn(x) of the Fourier series of the function /(x) converge to the function /(x) on average, i.e. according to the norm of space 6]. Definition. An orthonormal system ( is called complete in b2[ау b] if every function can be approximated on average with any accuracy by a linear combination of the form c sufficiently a large number terms, i.e. if for every function f(x) € b2[a, b\ and for any e > 0 there is natural number nq and numbers a\, a2y..., such that No From the above reasoning follows Theorem 7. If by orthonormalization the system ) is complete in space, the Fourier series of any function / over this system converges to f(x) on average, i.e. by norm It can be shown that the trigonometric system is complete in space. This implies the statement. Theorem 8. If a function /o its trigonometric Fourier series converges to it in average. 9.5. Closed systems. Completeness and closedness of systems Definition. An orthonormal system of functions \ is called closed if in the space Li\a, b) there is no non-zero function orthogonal to all functions. In the space L2\a, b\, the concepts of completeness and closedness of orthonormal systems coincide. Exercises 1. Expand the function in a Fourier series in the interval (-i-, x) 2. Expand the function 3 in a Fourier series in the interval (-tr, tr) 3. Expand the function 4 in a Fourier series in the interval (-tr, tr) into a Fourier series in the interval (-jt, tr) function 5. Expand the function f(x) = x + x into a Fourier series in the interval (-jt, tr). 6. Expand the function n into a Fourier series in the interval (-jt, tr) 7. Expand the function f(x) = sin2 x into a Fourier series in the interval (-tr, x). 8. Expand the function f(x) = y into a Fourier series in the interval (-tr, jt) 9. Expand the function f(x) = | sin x|. 10. Expand the function f(x) = § into a Fourier series in the interval (-π-, π). 11. Expand the function f(x) = sin § into a Fourier series in the interval (-tr, tr). 12. Expand the function f(x) = n -2x, given in the interval (0, x), into a Fourier series, extending it into the interval (-x, 0): a) in an even manner; b) in an odd way. 13. Expand the function /(x) = x2, given in the interval (0, x), into a Fourier series in sines. 14. Expand the function /(x) = 3, given in the interval (-2,2), into a Fourier series. 15. Expand the function f(x) = |x|, given in the interval (-1,1), into a Fourier series. 16. Expand the function f(x) = 2x, specified in the interval (0,1), into a Fourier series in sines.

Fourier series of periodic functions with period 2π.

The Fourier series allows us to study periodic functions by decomposing them into components. Alternating currents and stresses, displacements, speed and acceleration of crank mechanisms and acoustic waves are typical practical examples of the use of periodic functions in engineering calculations.

The Fourier series expansion is based on the assumption that all functions of practical significance in the interval -π ≤x≤ π can be expressed in the form of convergent trigonometric series (a series is considered convergent if the sequence of partial sums composed of its terms converges):

Standard (=ordinary) notation through the sum of sinx and cosx

f(x)=a o + a 1 cosx+a 2 cos2x+a 3 cos3x+...+b 1 sinx+b 2 sin2x+b 3 sin3x+...,

where a o, a 1,a 2,...,b 1,b 2,.. are real constants, i.e.

Where, for the range from -π to π, the coefficients of the Fourier series are calculated using the formulas:

The coefficients a o , a n and b n are called Fourier coefficients, and if they can be found, then series (1) is called the Fourier series corresponding to the function f (x). For series (1), the term (a 1 cosx+b 1 sinx) is called the first or fundamental harmonic,

Another way to write a series is to use the relation acosx+bsinx=csin(x+α)

f(x)=a o +c 1 sin(x+α 1)+c 2 sin(2x+α 2)+...+c n sin(nx+α n)

Where a o is a constant, with 1 =(a 1 2 +b 1 2) 1/2, with n =(a n 2 +b n 2) 1/2 - the amplitudes of the various components, and is equal to a n =arctg a n /b n.

For series (1), the term (a 1 cosx+b 1 sinx) or c 1 sin(x+α 1) is called the first or fundamental harmonic, (a 2 cos2x+b 2 sin2x) or c 2 sin(2x+α 2) called the second harmonic and so on.

To accurately represent a complex signal typically requires an infinite number of terms. However, in many practical problems it is sufficient to consider only the first few terms.

Fourier series of non-periodic functions with period 2π.

Expansion of non-periodic functions.

If the function f(x) is non-periodic, it means that it cannot be expanded into a Fourier series for all values ​​of x. However, it is possible to define a Fourier series representing a function over any range of width 2π.

If not specified periodic function, a new function can be constructed by selecting values ​​of f(x) within a certain range and repeating them outside that range at 2π intervals. Since the new function is periodic with period 2π, it can be expanded into a Fourier series for all values ​​of x. For example, the function f(x)=x is not periodic. However, if it is necessary to expand it into a Fourier series in the interval from o to 2π, then outside this interval a periodic function with a period of 2π is constructed (as shown in the figure below).

For non-periodic functions such as f(x)=x, the sum of the Fourier series is equal to the value of f(x) at all points in a given range, but it is not equal to f(x) for points outside the range. To find the Fourier series of a non-periodic function in the 2π range, the same formula of Fourier coefficients is used.

Even and odd functions.

They say a function y=f(x) is even if f(-x)=f(x) for all values ​​of x. Graphs of even functions are always symmetrical about the y-axis (that is, they are mirror images). Two examples of even functions: y=x2 and y=cosx.

A function y=f(x) is said to be odd if f(-x)=-f(x) for all values ​​of x. Graphs of odd functions are always symmetrical about the origin.

Many functions are neither even nor odd.

Fourier series expansion in cosines.

The Fourier series of an even periodic function f(x) with period 2π contains only cosine terms (i.e., no sine terms) and may include a constant term. Hence,

where are the coefficients of the Fourier series,

The Fourier series of an odd periodic function f(x) with period 2π contains only terms with sines (that is, it does not contain terms with cosines).

Hence,

where are the coefficients of the Fourier series,

Fourier series at half cycle.

If a function is defined for a range, say from 0 to π, and not just from 0 to 2π, it can be expanded in a series only in sines or only in cosines. The resulting Fourier series is called the half-cycle Fourier series.

If you want to obtain a half-cycle Fourier expansion of the cosines of the function f(x) in the range from 0 to π, then you need to construct an even periodic function. In Fig. Below is the function f(x)=x, built on the interval from x=0 to x=π. Since the even function is symmetrical about the f(x) axis, we draw line AB, as shown in Fig. below. If we assume that outside the considered interval the resulting triangular shape is periodic with a period of 2π, then the final graph looks like this: in Fig. below. Since we need to obtain the Fourier expansion in cosines, as before, we calculate the Fourier coefficients a o and a n

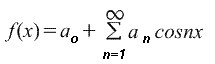
If you want to obtain a half-cycle Fourier expansion in terms of the sines of the function f(x) in the range from 0 to π, then you need to construct an odd periodic function. In Fig. Below is the function f(x)=x, built on the interval from x=0 to x=π. Since the odd function is symmetrical about the origin, we construct the line CD, as shown in Fig. If we assume that outside the considered interval the resulting sawtooth signal is periodic with a period of 2π, then the final graph has the form shown in Fig. Since we need to obtain the Fourier expansion of the half-cycle in terms of sines, as before, we calculate the Fourier coefficient. b

Fourier series for an arbitrary interval.

Expansion of a periodic function with period L.

The periodic function f(x) repeats as x increases by L, i.e. f(x+L)=f(x). The transition from the previously considered functions with a period of 2π to functions with a period of L is quite simple, since it can be done using a change of variable.

To find the Fourier series of the function f(x) in the range -L/2≤x≤L/2, we introduce a new variable u so that the function f(x) has a period of 2π relative to u. If u=2πx/L, then x=-L/2 for u=-π and x=L/2 for u=π. Also let f(x)=f(Lu/2π)=F(u). The Fourier series F(u) has the form

(The limits of integration can be replaced by any interval of length L, for example, from 0 to L)

Fourier series on a half-cycle for functions specified in the interval L≠2π.

For the substitution u=πх/L, the interval from x=0 to x=L corresponds to the interval from u=0 to u=π. Consequently, the function can be expanded into a series only in cosines or only in sines, i.e. into a Fourier series at half cycle.

The cosine expansion in the range from 0 to L has the form

Many processes occurring in nature and technology tend to repeat themselves at certain intervals. Such processes are called periodic and are mathematically described by periodic functions. Such functions include sin(x) , cos(x) , sin(wx), cos(wx) . The sum of two periodic functions, for example, a function of the form , generally speaking, is no longer periodic. But it can be proven that if the relation w 1 / w 2 is a rational number, then this sum is a periodic function.

The simplest periodic processes - harmonic oscillations - are described by periodic functions sin(wx) And cos(wx). More complex periodic processes are described by functions composed of either a finite or an infinite number of terms of the form sin(wx) And cos(wx).

Let's consider a functional series of the form:

This series is called trigonometric; numbers A 0 , b 0 , a 1 , b 1 ,A 2 , b 2 …, a n , b n ,… are called coefficients trigonometric series. Series (1) is often written as follows:

. (2)

Since the members of the trigonometric series (2) have a common period
, then the sum of the series, if it converges, is also a periodic function with period
.

Let's assume that the function f(x) is the sum of this series:

. (3)

In this case they say that the function f(x) is expanded into a trigonometric series. Assuming that this series converges uniformly on the interval
, you can determine its coefficients using the formulas:

,
,
. (4)

The coefficients of the series determined by these formulas are called Fourier coefficients.

Trigonometric series (2), the coefficients of which are determined by Fourier formulas (4), are called near Fourier, corresponding to the function f(x).

Thus, if a periodic function f(x) is the sum of a convergent trigonometric series, then this series is its Fourier series.

Formulas (4) show that the Fourier coefficients can be calculated for any integrable on the interval

-periodic function, i.e. For such a function one can always construct a Fourier series. But will this series converge to the function f(x) and under what conditions?

Recall that the function f(x), defined on the segment [ a; b] , is called piecewise smooth if it and its derivative have no more than a finite number of discontinuity points of the first kind.

The following theorem gives sufficient conditions for the decomposability of a function in a Fourier series.

Dirichlet's theorem. Let
-periodic function f(x) is piecewise smooth on
. Then its Fourier series converges to f(x) at each of its points of continuity and to the value 0,5(f(x+0)+ f(x-0)) at the breaking point.

Example 1.

Expand the function into a Fourier series f(x)= x, specified on the interval
.

Solution. This function satisfies the Dirichlet conditions and, therefore, can be expanded in a Fourier series. Using formulas (4) and the method of integration by parts
, let's find the Fourier coefficients:

Thus, the Fourier series for the function f(x) has a look.

How to insert mathematical formulas to the site?

If you ever need to add one or two mathematical formulas to a web page, then the easiest way to do this is as described in the article: mathematical formulas are easily inserted onto the site in the form of pictures that are automatically generated by Wolfram Alpha. In addition to simplicity, this universal method will help improve the visibility of the site in search engines. It has been working for a long time (and, I think, will work forever), but is already morally outdated.

If you constantly use mathematical formulas on your site, then I recommend that you use MathJax - a special JavaScript library that displays mathematical notation in web browsers using MathML, LaTeX or ASCIIMathML markup.

There are two ways to start using MathJax: (1) using a simple code, you can quickly connect a MathJax script to your website, which will be automatically loaded from a remote server at the right time (list of servers); (2) download the MathJax script from a remote server to your server and connect it to all pages of your site. The second method - more complex and time-consuming - will speed up the loading of your site's pages, and if the parent MathJax server becomes temporarily unavailable for some reason, this will not affect your own site in any way. Despite these advantages, I chose the first method as it is simpler, faster and does not require technical skills. Follow my example, and in just 5 minutes you will be able to use all the features of MathJax on your site.

You can connect the MathJax library script from a remote server using two code options taken from the main MathJax website or on the documentation page:

One of these code options needs to be copied and pasted into the code of your web page, preferably between tags and or immediately after the tag. According to the first option, MathJax loads faster and slows down the page less. But the second option automatically tracks and loads latest versions MathJax. If you insert the first code, it will need to be updated periodically. If you insert the second code, the pages will load more slowly, but you will not need to constantly monitor MathJax updates.

The easiest way to connect MathJax is in Blogger or WordPress: in the site control panel, add a widget designed to insert third-party JavaScript code, copy the first or second version of the download code presented above into it, and place the widget closer to the beginning of the template (by the way, this is not at all necessary , since the MathJax script is loaded asynchronously). That's it. Now learn the markup syntax of MathML, LaTeX, and ASCIIMathML, and you are ready to insert mathematical formulas into your site's web pages.

Any fractal is constructed according to a certain rule, which is consistently applied an unlimited number of times. Each such time is called an iteration.

The iterative algorithm for constructing a Menger sponge is quite simple: the original cube with side 1 is divided by planes parallel to its faces into 27 equal cubes. One central cube and 6 cubes adjacent to it along the faces are removed from it. The result is a set consisting of the remaining 20 smaller cubes. Doing the same with each of these cubes, we get a set consisting of 400 smaller cubes. Continuing this process endlessly, we get a Menger sponge.