O desvio padrão é um valor padrão. Parâmetros estatísticos
Em testes estatísticos de hipóteses, ao medir uma relação linear entre variáveis aleatórias.
Desvio padrão:
Desvio padrão (estimativa do desvio padrão variável aleatória O chão, as paredes ao nosso redor e o teto, x em relação a ela expectativa matemática com base em uma estimativa imparcial de sua variância):
onde está a dispersão; - O chão, as paredes ao nosso redor e o teto, eu o elemento da seleção; - tamanho da amostra; - média aritmética da amostra:
Deve-se notar que ambas as estimativas são tendenciosas. No caso geral, é impossível construir uma estimativa imparcial. No entanto, a estimativa baseada na estimativa de variância imparcial é consistente.
Regra dos três sigma
Regra dos três sigma() - quase todos os valores de uma variável aleatória normalmente distribuída estão no intervalo. Mais estritamente - com pelo menos 99,7% de confiança, o valor de uma variável aleatória normalmente distribuída está no intervalo especificado (desde que o valor seja verdadeiro e não obtido como resultado do processamento da amostra).
Se o verdadeiro valor for desconhecido, então não devemos usar, mas sim o Piso, as paredes ao nosso redor e o teto, é. Por isso, regra de três sigma é convertido na regra de três O chão, as paredes ao nosso redor e o teto, é .
Interpretação do valor do desvio padrão
Um grande valor do desvio padrão mostra uma grande dispersão dos valores do conjunto apresentado com o valor médio do conjunto; um valor pequeno, portanto, mostra que os valores do conjunto estão agrupados em torno do valor médio.
Por exemplo, temos três conjuntos de números: (0, 0, 14, 14), (0, 6, 8, 14) e (6, 6, 8, 8). Todos os três conjuntos possuem valores médios iguais a 7, e desvios padrão, respectivamente, iguais a 7, 5 e 1. O último conjunto possui um pequeno desvio padrão, pois os valores do conjunto estão agrupados em torno do valor médio; o primeiro conjunto tem o maior valor de desvio padrão - os valores dentro do conjunto divergem muito do valor médio.
De um modo geral, o desvio padrão pode ser considerado uma medida de incerteza. Por exemplo, em física, o desvio padrão é usado para determinar o erro de uma série de medições sucessivas de alguma quantidade. Este valor é muito importante para determinar a plausibilidade do fenômeno em estudo em comparação com o valor previsto pela teoria: se o valor médio das medições difere muito dos valores previstos pela teoria (grande desvio padrão), então os valores obtidos ou o método para obtê-los devem ser verificados novamente.
Uso pratico
Na prática, o desvio padrão permite determinar o quanto os valores de um conjunto podem diferir do valor médio.
Clima
Suponha que existam duas cidades com a mesma temperatura média máxima diária, mas uma está localizada no litoral e a outra no interior. Sabe-se que as cidades localizadas no litoral apresentam temperaturas máximas diurnas diferentes, mais baixas do que as cidades localizadas no interior. Portanto, o desvio padrão das temperaturas máximas diárias para uma cidade costeira será menor do que para a segunda cidade, apesar de o valor médio deste valor ser o mesmo, o que na prática significa que a probabilidade de que a temperatura máxima do ar em qualquer dia do ano será maior e diferente do valor médio, maior para uma cidade localizada no interior.
Esporte
Suponhamos que existam vários times de futebol que são avaliados de acordo com algum conjunto de parâmetros, por exemplo, o número de gols marcados e sofridos, chances de gol, etc. melhores valores Por mais parâmetros. Quanto menor for o desvio padrão da equipe para cada um dos parâmetros apresentados, mais previsível será o resultado da equipe; Por outro lado, a equipe com grande valor desvio padrão é difícil prever o resultado, que por sua vez é explicado pelo desequilíbrio, por exemplo, defesa forte, mas um ataque fraco.
A utilização do desvio padrão dos parâmetros das equipes permite, de uma forma ou de outra, prever o resultado de uma partida entre duas equipes, avaliando os pontos fortes e lados fracos comandos e, portanto, os métodos de luta escolhidos.
Análise técnica
Veja também
Literatura
| Este artigo foi proposto para exclusão.
Uma explicação dos motivos e a discussão correspondente podem ser encontradas na página Wikipedia: A ser excluído/17 de dezembro de 2012. |
* Borovikov, V. ESTATÍSTICA. A arte da análise de dados em um computador: Para profissionais / V. Borovikov. - São Petersburgo. : Pedro, 2003. - 688 p. - ISBN 5-272-00078-1.
| Indicadores estatísticos | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Descritivo Estatisticas |
|
||||||||||
| Estatística saída e exame hipóteses |
| ||||||||||
Definida como uma característica generalizante do tamanho da variação de uma característica no agregado. É igual à raiz quadrada do desvio quadrático médio dos valores individuais do atributo da média aritmética, ou seja, A raiz de e pode ser encontrada assim:
1. Para a linha primária:
2. Para as séries de variação:

A transformação da fórmula do desvio padrão traz-a para uma forma mais conveniente para cálculos práticos:
Desvio padrão determina o quanto, em média, as opções específicas se desviam de seu valor médio, e também é uma medida absoluta da variabilidade de uma característica e é expressa nas mesmas unidades das opções e, portanto, é bem interpretada.
Exemplos de como encontrar o desvio padrão: ,
Para características alternativas, a fórmula média desvio quadrado parece com isso:
![]()
onde p é a proporção de unidades da população que possuem determinada característica;
q é a proporção de unidades que não possuem essa característica.
O conceito de desvio linear médio
Média desvio linear é definido como a média aritmética dos valores absolutos dos desvios das opções individuais de .
1. Para a linha primária:

2. Para as séries de variação:

onde a soma n é soma das frequências das séries de variação.
Um exemplo de como encontrar o desvio linear médio:
A vantagem do desvio médio absoluto como medida de dispersão ao longo da faixa de variação é óbvia, uma vez que esta medida se baseia na consideração de todos os desvios possíveis. Mas este indicador tem desvantagens significativas. A rejeição arbitrária de sinais algébricos de desvios pode levar ao fato de que as propriedades matemáticas deste indicador estão longe de ser elementares. Isso torna muito difícil o uso do desvio médio absoluto na resolução de problemas que envolvem cálculos probabilísticos.
Assim, o desvio linear médio como medida de variação de uma característica raramente é utilizado na prática estatística, nomeadamente quando faz sentido do ponto de vista económico resumir indicadores sem ter em conta sinais. Com a sua ajuda, por exemplo, o volume de negócios é analisado Comércio exterior, composição dos trabalhadores, ritmo de produção, etc.
Quadrado médio
Média quadrada aplicada, por exemplo, para calcular o tamanho médio dos lados de n seções quadradas, os diâmetros médios de troncos, tubos, etc.
Quadrado médio simples. Se, ao substituir os valores individuais de uma característica por um valor médio, for necessário manter inalterada a soma dos quadrados dos valores originais, então a média será um valor médio quadrático.
É a raiz quadrada do quociente da divisão da soma dos quadrados dos valores dos atributos individuais pelo seu número:
O quadrado médio ponderado é calculado usando a fórmula:

onde f é o sinal de peso.
Cúbico médio
A cúbica média se aplica, por exemplo, ao determinar o comprimento médio de um lado e de cubos. Está dividido em dois tipos.
Média cúbica simples:


Ao calcular valores médios e dispersão em séries de distribuição intervalar, os valores verdadeiros do atributo são substituídos pelos valores centrais dos intervalos, que diferem da média aritmética dos valores incluídos no intervalo. Isso leva a um erro sistemático no cálculo da variância. V.F. Sheppard determinou que erro no cálculo da variação, causado pelo uso de dados agrupados, é 1/12 do quadrado do intervalo tanto na direção ascendente quanto descendente da variância.
Emenda Sheppard deve ser utilizado se a distribuição estiver próxima da normal, se referir a uma característica com natureza contínua de variação e se basear em uma quantidade significativa de dados iniciais (n > 500). Porém, pelo fato de que em alguns casos ambos os erros, agindo em direções diferentes, se compensam, às vezes é possível recusar a introdução de correções.
Quanto menor a variância e o desvio padrão, mais homogênea será a população e mais típica será a média.
Na prática da estatística, muitas vezes é necessário comparar variações de várias características. Por exemplo, é de grande interesse comparar variações na idade dos trabalhadores e nas suas qualificações, tempo de serviço e tamanho remunerações, custo e lucro, tempo de serviço e produtividade do trabalho, etc. Para tais comparações, os indicadores de variabilidade absoluta das características são inadequados: é impossível comparar a variabilidade da experiência profissional, expressa em anos, com a variação dos salários, expressa em rublos.
Para realizar tais comparações, bem como comparações da variabilidade de uma mesma característica em diversas populações com médias aritméticas diferentes, utiliza-se indicador relativo variação - coeficiente de variação.
Médias estruturais
Para caracterizar a tendência central nas distribuições estatísticas, muitas vezes é racional utilizar, juntamente com a média aritmética, um determinado valor da característica X, que, devido a certas características da sua localização na série de distribuição, pode caracterizar o seu nível.
Isto é especialmente importante quando em uma série de distribuição os valores extremos de uma característica têm limites pouco claros. A este respeito, uma determinação precisa da média aritmética é geralmente impossível ou muito difícil. Em tais casos nível médio pode ser determinado tomando, por exemplo, um valor de recurso localizado no meio de uma série de frequências ou que ocorre com mais frequência na série atual.
Tais valores dependem apenas da natureza das frequências, ou seja, da estrutura da distribuição. São típicos em localização em uma série de frequências, portanto tais valores são considerados como características do centro da distribuição e por isso receberam a definição de médias estruturais. Eles são usados para estudar estrutura interna e a estrutura da série de distribuição de valores de atributos. Esses indicadores incluem.
$X$. Para começar, vamos relembrar a seguinte definição:
Definição 1
População- um conjunto de objetos selecionados aleatoriamente de um determinado tipo, sobre os quais são realizadas observações para obter valores específicos de uma variável aleatória, realizadas em condições constantes ao estudar uma variável aleatória de um determinado tipo.
Definição 2
Variação geral- a média aritmética dos desvios quadrados dos valores da variante populacional em relação ao seu valor médio.
Deixe que os valores da opção $x_1,\ x_2,\dots ,x_k$ tenham, respectivamente, frequências $n_1,\ n_2,\dots ,n_k$. Em seguida, a variância geral é calculada usando a fórmula:
Vamos considerar um caso especial. Deixe todas as opções $x_1,\ x_2,\dots ,x_k$ serem diferentes. Neste caso $n_1,\ n_2,\dots ,n_k=1$. Descobrimos que neste caso a variância geral é calculada usando a fórmula:
Este conceito também está associado ao conceito de desvio padrão geral.
Definição 3
Desvio padrão geral
\[(\sigma )_g=\sqrt(D_g)\]
Variância da amostra
Seja-nos dada uma amostra populacional em relação a uma variável aleatória $X$. Para começar, vamos relembrar a seguinte definição:
Definição 4
População amostral-- parte de objetos selecionados da população em geral.
Definição 5
Variância da amostra-- média valores aritméticos opção de amostragem.
Deixe que os valores da opção $x_1,\ x_2,\dots ,x_k$ tenham, respectivamente, frequências $n_1,\ n_2,\dots ,n_k$. Em seguida, a variância da amostra é calculada usando a fórmula:
Vamos considerar um caso especial. Deixe todas as opções $x_1,\ x_2,\dots ,x_k$ serem diferentes. Neste caso $n_1,\ n_2,\dots ,n_k=1$. Descobrimos que neste caso a variância da amostra é calculada usando a fórmula:
Também relacionado a este conceito está o conceito de desvio padrão amostral.
Definição 6
Desvio padrão da amostra -- Raiz quadrada da variação geral:
\[(\sigma )_в=\sqrt(D_в)\]
Variância corrigida
Para encontrar a variância corrigida $S^2$ é necessário multiplicar a variância da amostra pela fração $\frac(n)(n-1)$, ou seja
Este conceito também está associado ao conceito de desvio padrão corrigido, que é encontrado pela fórmula:
No caso em que os valores das variantes não são discretos, mas representam intervalos, então nas fórmulas de cálculo das variâncias gerais ou amostrais, o valor de $x_i$ é considerado o valor do meio do intervalo para ao qual $x_i.$ pertence.
Um exemplo de problema para encontrar a variância e o desvio padrão
Exemplo 1
A população amostral é definida pela seguinte tabela de distribuição:
Imagem 1.
Vamos encontrar para isso a variância amostral, o desvio padrão amostral, a variância corrigida e o desvio padrão corrigido.
Para resolver este problema, primeiro fazemos uma tabela de cálculo:
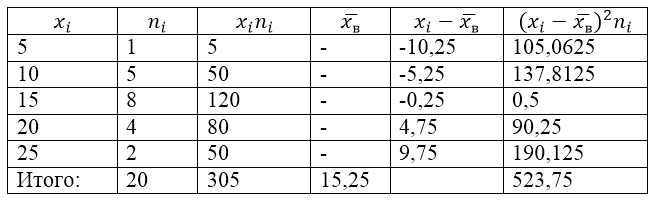
Figura 2.
O valor $\overline(x_в)$ (média amostral) na tabela é encontrado pela fórmula:
\[\overline(x_in)=\frac(\sum\limits^k_(i=1)(x_in_i))(n)\]
\[\overline(x_in)=\frac(\soma\limites^k_(i=1)(x_in_i))(n)=\frac(305)(20)=15,25\]
Vamos encontrar a variação da amostra usando a fórmula:
Desvio padrão da amostra:
\[(\sigma )_в=\sqrt(D_в)\aproximadamente 5,12\]
Variância corrigida:
\[(S^2=\frac(n)(n-1)D)_в=\frac(20)(19)\cdot 26,1875\aproximadamente 27,57\]
Desvio padrão corrigido.
De acordo com a pesquisa por amostragem, os depositantes foram agrupados de acordo com o tamanho do seu depósito no Sberbank da cidade:
Definir:
1) escopo de variação;
2) tamanho médio do depósito;
3) desvio linear médio;
4) dispersão;
5) desvio padrão;
6) coeficiente de variação das contribuições.
Solução:
Esta série de distribuição contém intervalos abertos. Nessas séries, o valor do intervalo do primeiro grupo é convencionalmente assumido como igual ao valor do intervalo do próximo, e o valor do intervalo do último grupo é igual ao valor do intervalo do o anterior.
O valor do intervalo do segundo grupo é igual a 200, portanto, o valor do primeiro grupo também é igual a 200. O valor do intervalo do penúltimo grupo é igual a 200, o que significa que o último intervalo também será tem um valor de 200.
1) Vamos definir a faixa de variação como a diferença entre o maior e o valor mais baixo sinal:
A faixa de variação no tamanho do depósito é de 1.000 rublos.
2) O valor médio da contribuição será determinado pela fórmula da média aritmética ponderada.
Vamos primeiro determinar o valor discreto do atributo em cada intervalo. Para fazer isso, usando a fórmula da média aritmética simples, encontramos os pontos médios dos intervalos.
O valor médio do primeiro intervalo será:

o segundo - 500, etc.
Vamos inserir os resultados do cálculo na tabela:
| Valor do depósito, esfregue. | Número de depositantes, f | Meio do intervalo, x | xf |
|---|---|---|---|
| 200-400 | 32 | 300 | 9600 |
| 400-600 | 56 | 500 | 28000 |
| 600-800 | 120 | 700 | 84000 |
| 800-1000 | 104 | 900 | 93600 |
| 1000-1200 | 88 | 1100 | 96800 |
| Total | 400 | - | 312000 |
O depósito médio no Sberbank da cidade será de 780 rublos:
3) O desvio linear médio é a média aritmética dos desvios absolutos dos valores individuais de uma característica da média geral:

O procedimento para calcular o desvio linear médio nas séries de distribuição intervalar é o seguinte:
1. Calcula-se a média aritmética ponderada, conforme indicado no n.º 2).
2. Os desvios absolutos da média são determinados:
3. Os desvios resultantes são multiplicados pelas frequências:
4. Encontre a soma dos desvios ponderados sem levar em conta o sinal:
5. A soma dos desvios ponderados é dividida pela soma das frequências:
É conveniente usar a tabela de dados de cálculo:
| Valor do depósito, esfregue. | Número de depositantes, f | Meio do intervalo, x | |||
|---|---|---|---|---|---|
| 200-400 | 32 | 300 | -480 | 480 | 15360 |
| 400-600 | 56 | 500 | -280 | 280 | 15680 |
| 600-800 | 120 | 700 | -80 | 80 | 9600 |
| 800-1000 | 104 | 900 | 120 | 120 | 12480 |
| 1000-1200 | 88 | 1100 | 320 | 320 | 28160 |
| Total | 400 | - | - | - | 81280 |

O desvio linear médio do tamanho do depósito dos clientes do Sberbank é de 203,2 rublos.
4) Dispersão é a média aritmética dos desvios quadrados do valor de cada atributo em relação à média aritmética.
O cálculo da variância nas séries de distribuição intervalar é realizado pela fórmula:

O procedimento para calcular a variância neste caso é o seguinte:
1. Determine a média aritmética ponderada, conforme indicado no parágrafo 2).
2. Encontre desvios da média:
3. Eleve ao quadrado o desvio de cada opção em relação à média:
4. Multiplique os quadrados dos desvios pelos pesos (frequências):
![]()
5. Resuma os produtos resultantes:
![]()
6. O valor resultante é dividido pela soma dos pesos (frequências):

Vamos colocar os cálculos em uma tabela:
| Valor do depósito, esfregue. | Número de depositantes, f | Meio do intervalo, x | |||
|---|---|---|---|---|---|
| 200-400 | 32 | 300 | -480 | 230400 | 7372800 |
| 400-600 | 56 | 500 | -280 | 78400 | 4390400 |
| 600-800 | 120 | 700 | -80 | 6400 | 768000 |
| 800-1000 | 104 | 900 | 120 | 14400 | 1497600 |
| 1000-1200 | 88 | 1100 | 320 | 102400 | 9011200 |
| Total | 400 | - | - | - | 23040000 |
Matemáticos e estatísticos sábios criaram um indicador mais confiável, embora com um propósito ligeiramente diferente - desvio linear médio. Este indicador caracteriza a medida de dispersão dos valores de um conjunto de dados em torno do seu valor médio.
Para mostrar a medida da dispersão dos dados, você deve primeiro decidir em relação ao que essa dispersão será calculada - geralmente este é o valor médio. Em seguida, você precisa calcular a que distância os valores do conjunto de dados analisado estão da média. É claro que cada valor corresponde a um determinado valor de desvio, mas interessa-nos a avaliação global, abrangendo toda a população. Portanto, o desvio médio é calculado usando a fórmula usual da média aritmética. Mas! Mas para calcular a média dos desvios, primeiro é necessário somá-los. E se somarmos números positivos e negativos, eles se anularão e sua soma tenderá a zero. Para evitar isso, todos os desvios são considerados módulo, ou seja, todos os números negativos tornam-se positivos. Agora o desvio médio mostrará uma medida generalizada da dispersão dos valores. Como resultado, o desvio linear médio será calculado pela fórmula:
a– desvio linear médio,
x– o indicador analisado, com um travessão acima – o valor médio do indicador,
n– o número de valores no conjunto de dados analisado,
Espero que o operador de soma não assuste ninguém.
O desvio linear médio calculado usando a fórmula especificada reflete o desvio absoluto médio do valor médio para uma determinada população.

Na foto, a linha vermelha é o valor médio. Os desvios de cada observação em relação à média são indicados por pequenas setas. Eles são tomados módulo e resumidos. Então tudo é dividido pelo número de valores.
Para completar o quadro, precisamos dar um exemplo. Digamos que haja uma empresa que produz mudas para pás. Cada corte deve ter 1,5 metros de comprimento, mas, mais importante, todos devem ser iguais ou pelo menos mais ou menos 5 cm. No entanto, trabalhadores descuidados cortarão 1,2 m ou 1,8 m. O diretor da empresa decidiu fazer uma análise estatística do comprimento dos cortes. Selecionei 10 peças e medi seu comprimento, encontrei a média e calculei o desvio linear médio. A média acabou sendo exatamente o que era necessário - 1,5 m, mas o desvio linear médio foi de 0,16 m. Acontece que cada corte é mais longo ou mais curto do que o necessário, em média, em 16 cm. trabalhadores. Na verdade, não vi nenhum uso real desse indicador, então eu mesmo criei um exemplo. No entanto, existe tal indicador nas estatísticas.
Dispersão
Tal como o desvio linear médio, a variância também reflete a extensão da dispersão dos dados em torno do valor médio.
A fórmula para calcular a variância é assim:
 (para séries de variação (variância ponderada))
(para séries de variação (variância ponderada))
 (para dados desagrupados (variância simples))
(para dados desagrupados (variância simples))
Onde: σ 2 – dispersão, XI– analisamos o indicador sq (o valor da característica), – o valor médio do indicador, f i – o número de valores no conjunto de dados analisado.
A dispersão é o quadrado médio dos desvios.
Primeiro, calcula-se o valor médio, depois a diferença entre cada valor original e médio é tomada, elevada ao quadrado, multiplicada pela frequência do valor do atributo correspondente, somada e depois dividida pelo número de valores na população.
Porém, em sua forma pura, como a média aritmética, ou índice, a dispersão não é utilizada. É antes um indicador auxiliar e intermediário que é utilizado para outros tipos de análise estatística.
Uma maneira simplificada de calcular a variância
![]()
Desvio padrão
Para usar a variância para análise de dados, é obtida a raiz quadrada da variância. Acontece que o chamado desvio padrão.

A propósito, o desvio padrão também é chamado de sigma – da letra grega que o denota.
O desvio padrão, obviamente, também caracteriza a medida de dispersão dos dados, mas agora (ao contrário da variância) pode ser comparado com os dados originais. Como regra, as medidas de raiz quadrada média nas estatísticas fornecem resultados mais precisos do que as lineares. Portanto, o desvio padrão é uma medida mais precisa da dispersão dos dados do que o desvio médio linear.






