Standartinis nuokrypis yra standartinė vertė. Statistiniai parametrai
Statistiškai tikrinant hipotezes, matuojant tiesinį ryšį tarp atsitiktinių dydžių.
Standartinis nuokrypis:
Standartinis nuokrypis (standartinio nuokrypio įvertinimas atsitiktinis kintamasis Grindys, sienos aplink mus ir lubos, x jos atžvilgiu matematinis lūkestis remiantis nešališku jo dispersijos įvertinimu):
kur yra dispersija; - Grindys, sienos aplink mus ir lubos, i atrankos elementas; - imties dydis; - imties aritmetinis vidurkis:
Reikėtų pažymėti, kad abu vertinimai yra šališki. Bendruoju atveju nešališko įvertinimo sudaryti neįmanoma. Tačiau įvertinimas, pagrįstas nešališku dispersijos įvertinimu, yra nuoseklus.
Trijų sigmų taisyklė
Trijų sigmų taisyklė() - beveik visos normaliai paskirstyto atsitiktinio dydžio reikšmės yra intervale. Griežčiau – esant ne mažesniam kaip 99,7% pasikliovimui, normaliai pasiskirstyto atsitiktinio dydžio reikšmė yra nurodytame intervale (su sąlyga, kad reikšmė yra teisinga, o ne gauta apdorojant imtį).
Jei tikroji vertė nežinoma, turėtume naudoti ne grindis, sienas aplink mus ir lubas, s. Taigi, trijų taisyklė sigma paverčiama trijų taisykle: grindys, sienos aplink mus ir lubos, s .
Standartinio nuokrypio vertės aiškinimas
Didelė standartinio nuokrypio reikšmė rodo didelį pateikto rinkinio verčių sklaidą su vidutine rinkinio verte; atitinkamai maža reikšmė rodo, kad rinkinio reikšmės sugrupuotos aplink vidurinę vertę.
Pavyzdžiui, turime tris skaičių rinkinius: (0, 0, 14, 14), (0, 6, 8, 14) ir (6, 6, 8, 8). Visų trijų rinkinių vidutinės vertės yra lygios 7, o standartiniai nuokrypiai atitinkamai yra lygūs 7, 5 ir 1. Paskutinis rinkinys turi nedidelį standartinį nuokrypį, nes rinkinio reikšmės yra sugrupuotos pagal vidutinę vertę; pirmasis rinkinys turi didžiausią standartinio nuokrypio vertę - rinkinio vertės labai skiriasi nuo vidutinės vertės.
Bendrąja prasme standartinis nuokrypis gali būti laikomas neapibrėžtumo matu. Pavyzdžiui, fizikoje standartinis nuokrypis naudojamas tam tikro dydžio nuoseklių matavimų paklaidai nustatyti. Ši reikšmė yra labai svarbi nustatant tiriamo reiškinio tikimybę, lyginant su teorijos numatytu dydžiu: jei vidutinė matavimų vertė labai skiriasi nuo teorijos numatytų verčių (didelis standartinis nuokrypis), tada reikia dar kartą patikrinti gautas vertes arba jų gavimo būdą.
Praktinis naudojimas
Praktiškai standartinis nuokrypis leidžia nustatyti, kiek rinkinio vertės gali skirtis nuo vidutinės vertės.
Klimatas
Tarkime, kad yra dviejuose miestuose, kurių vidutinė maksimali paros temperatūra yra vienoda, tačiau vienas yra pakrantėje, o kitas – sausumoje. Yra žinoma, kad pakrantėje esančiuose miestuose yra daug skirtingų maksimalių dienos temperatūrų, kurios yra žemesnės nei miestuose, esančiuose sausumoje. Todėl pakrantės miesto didžiausios paros temperatūros standartinis nuokrypis bus mažesnis nei antrojo miesto, nepaisant to, kad vidutinė šios vertės reikšmė yra tokia pati, o tai praktiškai reiškia, kad tikimybė, kad maksimali oro temperatūra bet kuri tam tikra metų diena bus didesnė nei vidutinė vertė, didesnė miestui, esančiam viduje.
Sportas
Tarkime, kad yra kelios futbolo komandos, kurios vertinamos pagal tam tikrus parametrus, pavyzdžiui, įmuštų ir praleistų įvarčių skaičių, progas įmušti ir pan. Labiausiai tikėtina, kad geriausia šios grupės komanda turės geriausios vertybės Autorius daugiau parametrus. Kuo mažesnis kiekvieno pateikto parametro standartinis nuokrypis, tuo labiau nuspėjamas komandos rezultatas. Kita vertus, komanda su Gera vertė standartinį nuokrypį sunku nuspėti rezultatą, o tai savo ruožtu paaiškinama disbalansu, pvz. stipri gynyba, bet silpna ataka.
Komandos parametrų standartinio nuokrypio naudojimas leidžia vienu ar kitu laipsniu numatyti dviejų komandų rungtynių rezultatą, įvertinant stipriąsias ir silpnosios pusės komandas, taigi ir pasirinktus kovos būdus.
Techninė analizė
taip pat žr
Literatūra
| Šį straipsnį siūloma išbraukti.
Priežasčių paaiškinimą ir atitinkamą diskusiją rasite puslapyje Vikipedija: bus ištrinta / 2012 m. gruodžio 17 d. |
* Borovikovas, V. STATISTIKA. Duomenų analizės kompiuteriu menas: Profesionalams / V. Borovikovas. - Sankt Peterburgas. : Petras, 2003. - 688 p. - ISBN 5-272-00078-1.
| Statistiniai rodikliai | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Aprašomasis statistika |
|
||||||||||
| Statistiniai išvestis ir apžiūra hipotezes |
| ||||||||||
Apibrėžiama kaip apibendrinanti bruožo kitimo dydžio charakteristika visumoje. Jis lygus atskirų požymio verčių vidutinio kvadratinio nuokrypio nuo aritmetinio vidurkio kvadratinei šakniai, t.y. Ir šaknis galima rasti taip:
1. Pirminei eilutei:
2. Variacijų serijai:

Transformavus standartinio nuokrypio formulę, ji tampa patogesnė praktiniams skaičiavimams:
Standartinis nuokrypis nustato, kiek vidutiniškai konkrečios galimybės nukrypsta nuo jų vidutinės vertės, taip pat yra absoliutus charakteristikos kintamumo matas ir yra išreiškiamas tais pačiais vienetais kaip ir parinktys, todėl yra gerai interpretuojamas.
Standartinio nuokrypio nustatymo pavyzdžiai: ,
Alternatyvioms charakteristikoms – vidutinė formulė kvadratinis nuokrypis atrodo taip:
![]()
čia p – vienetų, turinčių tam tikrą požymį, dalis populiacijoje;
q yra vienetų, kurie neturi šios charakteristikos, dalis.
Vidutinio tiesinio nuokrypio samprata
Vidutinis tiesinis nuokrypis apibrėžiamas kaip atskirų variantų nuokrypių nuo absoliučių verčių aritmetinis vidurkis.
1. Pirminei eilutei:

2. Variacijų serijai:

kur yra suma n variacijų eilučių dažnių suma.
Vidutinio tiesinio nuokrypio nustatymo pavyzdys:
Vidutinio absoliutaus nuokrypio, kaip dispersijos matavimo svyravimo diapazone, pranašumas yra akivaizdus, nes šis matas pagrįstas visų galimų nuokrypių įvertinimu. Tačiau šis rodiklis turi reikšmingų trūkumų. Savavališkas algebrinių nukrypimų ženklų atmetimas gali lemti tai, kad matematinės šio rodiklio savybės toli gražu nėra elementarios. Dėl to labai sunku naudoti vidutinį absoliutų nuokrypį sprendžiant problemas, susijusias su tikimybiniais skaičiavimais.
Todėl vidutinis tiesinis nuokrypis kaip charakteristikos kitimo matas statistikos praktikoje naudojamas retai, būtent tada, kai rodiklių sumavimas neatsižvelgiant į ženklus yra ekonomiškai prasmingas. Su jo pagalba, pavyzdžiui, analizuojama apyvarta užsienio prekyba, darbuotojų sudėtis, gamybos ritmas ir kt.
Vidutinis kvadratas
Taikomas vidutinis kvadratas, pavyzdžiui, apskaičiuoti vidutinį n kvadratinių sekcijų kraštinių dydį, vidutinius kamienų, vamzdžių skersmenis ir kt. Jis skirstomas į du tipus.
Paprastas vidutinis kvadratas. Jei pakeičiant atskiras charakteristikos reikšmes vidutine verte, pradinių verčių kvadratų suma turi likti nepakitusi, tada vidurkis bus kvadratinis vidurkis.
Tai yra kvadratinė šaknis iš atskirų atributų verčių kvadratų sumos dalijimo iš jų skaičiaus:
Svertinis vidutinis kvadratas apskaičiuojamas pagal formulę:

kur f yra svorio ženklas.
Vidutinis kub
Taikomas vidutinis kub, pavyzdžiui, nustatant vidutinį kraštinės ir kubelių ilgį. Jis skirstomas į du tipus.
Vidutinis kubinis paprastas:


Skaičiuojant vidutines vertes ir dispersiją intervalų pasiskirstymo eilutėse, tikrosios požymio reikšmės pakeičiamos centrinėmis intervalų reikšmėmis, kurios skiriasi nuo į intervalą įtrauktų reikšmių aritmetinio vidurkio. Dėl to skaičiuojant dispersiją atsiranda sisteminė klaida. V.F. Sheppard tai nusprendė dispersijos skaičiavimo klaida, kurį sukelia sugrupuotų duomenų naudojimas, yra 1/12 intervalo kvadrato tiek dispersijos aukštyn, tiek žemyn kryptimi.
Sheppard pataisa turėtų būti naudojamas, jei pasiskirstymas yra artimas normaliam, yra susijęs su charakteristika, kurios kitimas yra nuolatinis, ir yra pagrįstas dideliu pradinių duomenų kiekiu (n > 500). Tačiau remiantis tuo, kad kai kuriais atvejais abi klaidos, veikiančios skirtingomis kryptimis, viena kitą kompensuoja, kartais galima atsisakyti įvesti pataisas.
Kuo mažesnė dispersija ir standartinis nuokrypis, tuo populiacija homogeniškesnė ir vidurkis bus tipiškesnis.
Statistikos praktikoje dažnai atsiranda poreikis palyginti įvairių charakteristikų variacijas. Pavyzdžiui, labai įdomu palyginti darbuotojų amžiaus ir jų kvalifikacijos, darbo stažo ir dydžio svyravimus darbo užmokesčio, sąnaudos ir pelnas, darbo stažas ir darbo našumas ir kt. Tokiems palyginimams netinka absoliutaus charakteristikų kintamumo rodikliai: neįmanoma palyginti darbo stažo kintamumo, išreikšto metais, su darbo užmokesčio kitimu rubliais.
Tokiems palyginimams atlikti, taip pat tos pačios charakteristikos kintamumo palyginimui keliose populiacijose su skirtingais aritmetiniais vidurkiais, naudojamas santykinis rodiklis variacija – variacijos koeficientas.
Struktūriniai vidurkiai
Centrinei statistinių skirstinių tendencijai apibūdinti dažnai racionalu kartu su aritmetiniu vidurkiu naudoti tam tikrą charakteristikos X reikšmę, kuri dėl tam tikrų jos vietos skirstinio eilutėje ypatumų gali apibūdinti jos lygį.
Tai ypač svarbu, kai pasiskirstymo serijoje charakteristikos kraštutinės reikšmės turi neaiškias ribas. Šiuo atžvilgiu tiksliai nustatyti aritmetinį vidurkį paprastai neįmanoma arba labai sunku. Tokiais atvejais vidutinis lygis galima nustatyti imant, pavyzdžiui, ypatybės reikšmę, esančią dažnių serijos viduryje arba kuri dažniausiai pasitaiko dabartinėse serijose.
Tokios reikšmės priklauso tik nuo dažnių pobūdžio, t.y. nuo pasiskirstymo struktūros. Jie yra tipiški vietoje dažnių serijoje, todėl tokios vertės laikomos pasiskirstymo centro charakteristikomis ir todėl gavo struktūrinių vidurkių apibrėžimą. Jie naudojami mokytis vidinė struktūra ir atributų reikšmių paskirstymo serijos struktūra. Tokie rodikliai apima.
$X$. Pirmiausia prisiminkime šį apibrėžimą:
1 apibrėžimas
Gyventojų skaičius- atsitiktinai atrinktų tam tikro tipo objektų rinkinys, kurio stebėjimai atliekami siekiant gauti konkrečias atsitiktinio dydžio reikšmes, atliekamos pastoviomis sąlygomis tiriant vieną tam tikro tipo atsitiktinį kintamąjį.
2 apibrėžimas
Bendra dispersija- populiacijos varianto verčių nukrypimų kvadratu nuo jų vidutinės vertės aritmetinis vidurkis.
Tegul parinkties $x_1,\ x_2,\dots ,x_k$ reikšmės turi atitinkamai dažnius $n_1,\n_2,\dots ,n_k$. Tada bendroji dispersija apskaičiuojama pagal formulę:
Panagrinėkime ypatingą atvejį. Tegul visos parinktys $x_1,\ x_2,\dots ,x_k$ skiriasi. Šiuo atveju $n_1,\ n_2,\dots ,n_k=1$. Pastebime, kad šiuo atveju bendroji dispersija apskaičiuojama naudojant formulę:
Ši sąvoka taip pat siejama su bendrojo standartinio nuokrypio sąvoka.
3 apibrėžimas
Bendras standartinis nuokrypis
\[(\sigma )_g=\sqrt(D_g)\]
Imties dispersija
Pateikiame pavyzdinę populiaciją atsitiktinio dydžio $X$ atžvilgiu. Pirmiausia prisiminkime šį apibrėžimą:
4 apibrėžimas
Imties populiacija-- dalis atrinktų objektų iš bendrosios populiacijos.
5 apibrėžimas
Imties dispersija-- vidutinis aritmetines vertes mėginių ėmimo galimybė.
Tegul parinkties $x_1,\ x_2,\dots ,x_k$ reikšmės turi atitinkamai dažnius $n_1,\n_2,\dots ,n_k$. Tada imties dispersija apskaičiuojama pagal formulę:
Panagrinėkime ypatingą atvejį. Tegul visos parinktys $x_1,\ x_2,\dots ,x_k$ skiriasi. Šiuo atveju $n_1,\ n_2,\dots ,n_k=1$. Pastebime, kad šiuo atveju imties dispersija apskaičiuojama naudojant formulę:
Taip pat su šia sąvoka susijusi imties standartinio nuokrypio samprata.
6 apibrėžimas
Mėginio standartinis nuokrypis -- Kvadratinė šaknis iš bendros dispersijos:
\[(\sigma )_в=\sqrt(D_в)\]
Pataisyta dispersija
Norint rasti pataisytą dispersiją $S^2$, imties dispersiją reikia padauginti iš trupmenos $\frac(n)(n-1)$, tai yra
Ši sąvoka taip pat siejama su pakoreguoto standartinio nuokrypio sąvoka, kuri randama pagal formulę:
Tuo atveju, kai variantų reikšmės nėra diskrečios, o reiškia intervalus, tada bendrųjų arba imties dispersijų skaičiavimo formulėse $x_i$ reikšmė laikoma intervalo vidurio reikšme. kuriai priklauso $x_i.$.
Problemos pavyzdys, kaip rasti dispersiją ir standartinį nuokrypį
1 pavyzdys
Imties visuma apibrėžiama pagal šią paskirstymo lentelę:
1 paveikslas.
Raskime imties dispersiją, imties standartinį nuokrypį, pataisytą dispersiją ir pataisytą standartinį nuokrypį.
Norėdami išspręsti šią problemą, pirmiausia sudarome skaičiavimo lentelę:
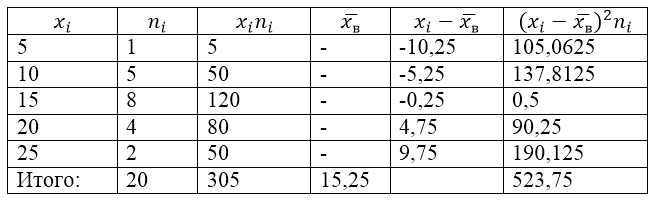
2 pav.
Vertė $\overline(x_в)$ (pavyzdžio vidurkis) lentelėje randama pagal formulę:
\[\overline(x_in)=\frac(\sum\limits^k_(i=1)(x_in_i))(n)\]
\[\overline(x_in)=\frac(\sum\limits^k_(i=1)(x_in_i))(n)=\frac(305)(20)=15,25\]
Raskime imties dispersiją naudodami formulę:
Standartinio nuokrypio pavyzdys:
\[(\sigma )_в=\sqrt(D_в)\apytiksliai 5,12\]
Pataisyta dispersija:
\[(S^2=\frac(n)(n-1)D)_в=\frac(20)(19)\cdot 26.1875\apytiksliai 27.57\]
Pataisytas standartinis nuokrypis.
Remiantis imties apklausa, indėlininkai buvo suskirstyti į grupes pagal jų indėlio dydį miesto Sberbanke:
Apibrėžkite:
1) variacijos apimtis;
2) vidutinis indėlio dydis;
3) vidutinis tiesinis nuokrypis;
4) dispersija;
5) standartinis nuokrypis;
6) įmokų variacijos koeficientas.
Sprendimas:
Šioje paskirstymo serijoje yra atviri intervalai. Tokiose serijose sutartinai daroma prielaida, kad pirmosios grupės intervalo reikšmė yra lygi kitos grupės intervalo reikšmei, o paskutinės grupės intervalo reikšmė yra lygi šios grupės intervalo reikšmei. ankstesnis.
Antrosios grupės intervalo reikšmė lygi 200, todėl pirmosios grupės reikšmė taip pat lygi 200. Priešpaskutinės grupės intervalo reikšmė lygi 200, vadinasi, bus ir paskutinis intervalas. kurių vertė 200.
1) Apibrėžkime kitimo diapazoną kaip skirtumą tarp didžiausio ir mažiausia vertėženklas:
Indėlio dydžio svyravimo diapazonas yra 1000 rublių.
2) Vidutinis įnašo dydis bus nustatytas naudojant svertinio aritmetinio vidurkio formulę.
Pirmiausia nustatykime diskrečiąją atributo reikšmę kiekviename intervale. Norėdami tai padaryti, naudodami paprastą aritmetinio vidurkio formulę, randame intervalų vidurio taškus.
Vidutinė pirmojo intervalo vertė bus:

antrasis - 500 ir kt.
Įveskime skaičiavimo rezultatus į lentelę:
| Indėlio suma, patrinkite. | Indėlininkų skaičius, f | Intervalo vidurys, x | xf |
|---|---|---|---|
| 200-400 | 32 | 300 | 9600 |
| 400-600 | 56 | 500 | 28000 |
| 600-800 | 120 | 700 | 84000 |
| 800-1000 | 104 | 900 | 93600 |
| 1000-1200 | 88 | 1100 | 96800 |
| Iš viso | 400 | - | 312000 |
Vidutinis indėlis miesto „Sberbank“ bus 780 rublių:
3) Vidutinis tiesinis nuokrypis yra individualių charakteristikų verčių absoliučių nuokrypių nuo bendro vidurkio aritmetinis vidurkis:

Vidutinio tiesinio nuokrypio intervalų pasiskirstymo eilutėse apskaičiavimo procedūra yra tokia:
1. Svertinis aritmetinis vidurkis apskaičiuojamas, kaip parodyta 2 dalyje).
2. Nustatomi absoliutūs nuokrypiai nuo vidurkio:
3. Gauti nuokrypiai dauginami iš dažnių:
4. Raskite svertinių nuokrypių sumą neatsižvelgdami į ženklą:
5. Svertinių nuokrypių suma padalinama iš dažnių sumos:
Patogu naudoti skaičiavimo duomenų lentelę:
| Indėlio suma, patrinkite. | Indėlininkų skaičius, f | Intervalo vidurys, x | |||
|---|---|---|---|---|---|
| 200-400 | 32 | 300 | -480 | 480 | 15360 |
| 400-600 | 56 | 500 | -280 | 280 | 15680 |
| 600-800 | 120 | 700 | -80 | 80 | 9600 |
| 800-1000 | 104 | 900 | 120 | 120 | 12480 |
| 1000-1200 | 88 | 1100 | 320 | 320 | 28160 |
| Iš viso | 400 | - | - | - | 81280 |

Vidutinis „Sberbank“ klientų indėlio dydžio tiesinis nuokrypis yra 203,2 rubliai.
4) Dispersija yra kiekvienos požymio reikšmės kvadratinių nuokrypių nuo aritmetinio vidurkio aritmetinis vidurkis.
Intervalų pasiskirstymo eilučių dispersijos apskaičiavimas atliekamas naudojant formulę:

Šiuo atveju dispersijos apskaičiavimo procedūra yra tokia:
1. Nustatykite svertinį aritmetinį vidurkį, kaip parodyta 2 pastraipoje).
2. Raskite nuokrypius nuo vidurkio:
3. Palyginkite kiekvienos parinkties nuokrypį nuo vidurkio kvadratu:
4. Padauginkite nuokrypių kvadratus iš svorių (dažnių):
![]()
5. Susumuokite gautus produktus:
![]()
6. Gauta suma padalinama iš svorių (dažnių) sumos:

Sudėkime skaičiavimus į lentelę:
| Indėlio suma, patrinkite. | Indėlininkų skaičius, f | Intervalo vidurys, x | |||
|---|---|---|---|---|---|
| 200-400 | 32 | 300 | -480 | 230400 | 7372800 |
| 400-600 | 56 | 500 | -280 | 78400 | 4390400 |
| 600-800 | 120 | 700 | -80 | 6400 | 768000 |
| 800-1000 | 104 | 900 | 120 | 14400 | 1497600 |
| 1000-1200 | 88 | 1100 | 320 | 102400 | 9011200 |
| Iš viso | 400 | - | - | - | 23040000 |
Išmintingi matematikai ir statistikai sugalvojo patikimesnį rodiklį, nors šiek tiek kitokiu tikslu - vidutinis tiesinis nuokrypis. Šis rodiklis apibūdina duomenų rinkinio verčių sklaidos pagal jų vidutinę vertę matą.
Norėdami parodyti duomenų sklaidos matą, pirmiausia turite nuspręsti, pagal ką ši sklaida bus apskaičiuojama – paprastai tai yra vidutinė vertė. Tada turite apskaičiuoti, kiek analizuojamų duomenų rinkinio reikšmės yra nuo vidurkio. Aišku, kad kiekviena reikšmė atitinka tam tikrą nuokrypio reikšmę, bet mus domina bendras vertinimas, apimantis visą populiaciją. Todėl vidutinis nuokrypis apskaičiuojamas naudojant įprastą aritmetinio vidurkio formulę. Bet! Tačiau norint apskaičiuoti nuokrypių vidurkį, pirmiausia juos reikia pridėti. Ir jei pridėsime teigiamus ir neigiamus skaičius, jie panaikins vienas kitą ir jų suma bus linkusi į nulį. Norint to išvengti, visi nuokrypiai imami modulo, tai yra, visi neigiami skaičiai tampa teigiami. Dabar vidutinis nuokrypis parodys apibendrintą reikšmių sklaidos matą. Dėl to vidutinis tiesinis nuokrypis bus apskaičiuojamas pagal formulę:
a- vidutinis tiesinis nuokrypis,
x– analizuojamas rodiklis, brūkšneliu aukščiau – vidutinė rodiklio reikšmė,
n– analizuojamo duomenų rinkinio verčių skaičius,
Tikiuosi, kad sumavimo operatorius nieko negąsdina.
Vidutinis tiesinis nuokrypis, apskaičiuotas naudojant nurodytą formulę, atspindi vidutinį absoliutų nuokrypį nuo konkrečios populiacijos vidutinės vertės.

Nuotraukoje raudona linija yra vidutinė vertė. Kiekvieno stebėjimo nuokrypiai nuo vidurkio žymimi mažomis rodyklėmis. Jie imami modulo ir sumuojami. Tada viskas padalijama iš reikšmių skaičiaus.
Norėdami užbaigti paveikslėlį, turime pateikti pavyzdį. Tarkime, yra įmonė, kuri gamina auginius kastuvams. Kiekvienas kirtimas turi būti 1,5 metro ilgio, bet dar svarbiau, kad jie visi būtų vienodi arba bent jau plius minus 5 cm. Tačiau neatsargūs darbuotojai nukirs 1,2 m arba 1,8 m. Įmonės direktorius nusprendė atlikti statistinę kirtimų ilgio analizę. Išsirinkau 10 vienetų ir išmatavau jų ilgį, suradau vidurkį ir paskaičiavau vidutinį tiesinį nuokrypį. Vidurkis pasirodė kaip tik tiek, kiek reikėjo – 1,5 m. Bet vidutinis tiesinis nuokrypis buvo 0,16 m. Taigi, kiekvienas pjūvis yra ilgesnis arba trumpesnis nei reikia vidutiniškai 16 cm darbininkai . Tiesą sakant, realaus šio rodiklio panaudojimo nemačiau, todėl pats sugalvojau pavyzdį. Tačiau statistikoje toks rodiklis yra.
Sklaida
Kaip ir vidutinis tiesinis nuokrypis, dispersija taip pat atspindi duomenų sklaidos apie vidutinę vertę mastą.
Dispersijos skaičiavimo formulė atrodo taip:
 (variacijų serijai (svertinis dispersija))
(variacijų serijai (svertinis dispersija))
 (nesugrupuotiems duomenims (paprasta dispersija))
(nesugrupuotiems duomenims (paprasta dispersija))
kur: σ 2 – dispersija, Xi– analizuojame kvadratinį rodiklį (charakteristikos reikšmę), – rodiklio vidutinę reikšmę, f i – reikšmių skaičių analizuojamame duomenų rinkinyje.
Dispersija yra vidutinis nuokrypių kvadratas.
Pirma, apskaičiuojama vidutinė vertė, tada imamas skirtumas tarp kiekvienos pradinės ir vidutinės vertės, pakeliamas kvadratas, padauginamas iš atitinkamo požymio reikšmės dažnio, pridedamas ir padalinamas iš populiacijos reikšmių skaičiaus.
Tačiau gryna forma, tokia kaip aritmetinis vidurkis arba indeksas, dispersija nenaudojama. Tai veikiau pagalbinis ir tarpinis rodiklis, naudojamas kitų tipų statistinei analizei.
Supaprastintas dispersijos skaičiavimo būdas
![]()
Standartinis nuokrypis
Norint naudoti dispersiją duomenų analizei, imama dispersijos kvadratinė šaknis. Pasirodo, vadinamasis standartinis nuokrypis.

Beje, standartinis nuokrypis dar vadinamas sigma – nuo jį žyminčios graikiškos raidės.
Standartinis nuokrypis, žinoma, taip pat apibūdina duomenų sklaidos matą, tačiau dabar (skirtingai nuo dispersijos) jį galima palyginti su pradiniais duomenimis. Paprastai vidutiniai kvadratiniai matai statistikoje duoda tikslesnius rezultatus nei tiesiniai. Todėl standartinis nuokrypis yra tikslesnis duomenų sklaidos matas nei tiesinis vidutinis nuokrypis.






